Traçats bàsics de la secció aùria.

Què és la "secció aùria" d'un segment?  :   

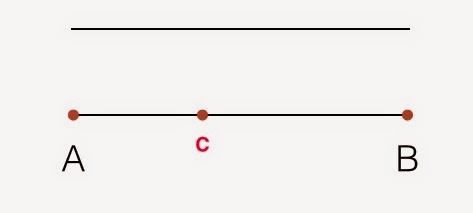
Es tracta de dividir un segment en dues parts desiguals,  però de manera molt precisa i seguint un traçat geomètric definit expressament per a això.  Com a resultat s'obté una dividisió proporcional del segment en dues fraccions que compleixen una condició molt curiosa:

Si es divideix la llargària de la porció més gran del segment fragmentat (C-B) entre la llargària de la porció més petita (A-C),  el resultat que obtenim és el mateix que si dividim la llargària total del segment   (A-B)  entre la llargària del fragment més gran  (C-B).   Aquest resultat donarà sempre el mateix nombre irracional que anomenem  Fi  i que simbolitzem amb la lletra grega    Φ.  És el també anomenat "nombre d'or"=  1,61803...  

(Vegeu també  l'entrada "El nombre d'or"  de 26/ 01/ 2015 en aquest mateix blog).  

Nature by Numbers - Cristobal Vila from Natalia Godoy on Vimeo.

 Com trobem aquest punt de divisió àuria?:

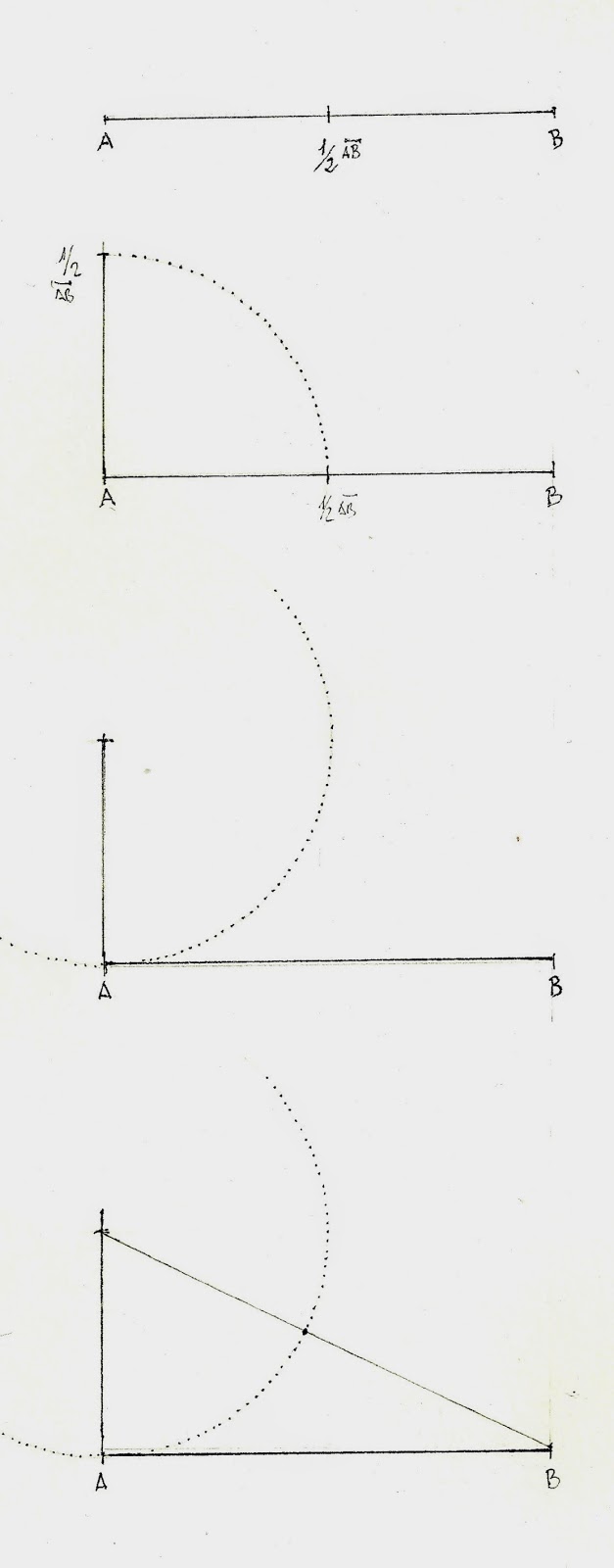
1-  Es divideix el segment inicial per la meitat.



2-  Prenem aquesta mesura  (1/2 segment AB) i la traslladem a un dels seus extrems,  en posició vertical,  perpendicular al segment inicial.







3-  El punt (1/2 AB) que hem situat en posició vertical serà ara el centre d'una circumferència de radi igual a aquesta línia dibuixada  (1/2 AB  -  A),  i un cop traçada serà,  per tant, tangent al segment inicial,  per aquest extrem.








4-  A continuació,  s'uneix mitjançant una recta el centre d'aquesta circumferència amb l'extrem oposat del segment inicial  (Unim el centre de la circumferència amb el punt B).
Sobre la circumferència ens apareix un punt d'intersecció entre la circumferència i la línia traçada.  Aquest punt és determinant (l'anomenarem, per exemple: C).

5- Amb el compàs i fent centre a B baixem el punt C a sobre del segment inicial:   Aquest punt C divideix ara el segment inicial en secció àuria.









6-  Si ara volem crear un rectangle auri partint d'aquest mateix segment,  només hem de dibuixar en vertical els costats del rectangle, fent que la seva amb alçada sigui igual a la mida C-B.








7-  S'obté el rectangle auri ABCD





Però també podríem haver obtingut aquest rectangle fent el següent traçat:

Rectangle auri a partir del quadrat:

1-  Un cop tenim el segment AB dividit en secció àuria,  tracem el quadrat de costats cB, BC, etc.
2-  Dividim verticalment el quadrat en dues meitats iguals.
3-  Tracem la "semidiagonal" del quadrat (La recta que uneix el punt mig del costat cB  amb un vertex oposat).
4- Amb el compàs, prenent aquesta semidiagonal com a radi,  tracem l'arc que baixa fins el punt A.
Des d'aquí acabem de dibuixar el rectangle auri.


                                     (Aquesta operació es pot fer sempre, partint de qualsevol quadrat)


Aplicació d'aquests traçats en la composició i en l'anàlisi formal de les obres d'art:

Una de les aplicaciones més interessants d'aquests traçats geomètrics es produeix quan s'utilitza la secció àuria per a dissenyar de manera equilibrada i harmònica una imatge o una composició d'elements.  
També,  quan analitzem formalment una obra pictòrica o escultòrica,  podem intentar descubrir si l'autor ha utilitzat la secció àuria com a base de la seva estructura.

                                          Georges de la Tour. El trampós de l'as de diamants

Podem começar per traçar els eixos derivats de dividir segons la secció àuria els costats del quadre.  Si comencem per trobar dos eixos,  un pel costat llarg i l'altre pel costat curt,  podrem traçar després els altres dos eixos simètrics amb tota facilitat.

Més enllà d'aquesta senzilla operació, i amb una mica més d'experiència,  l'anàlisi formal que explora totes les relacions àurees del quadre pot endinsar-se en molta més profunditat.

Anàlisi proposat per Bernard Rancillac al llibre Ver y Comprender LA PINTURA,
  ediciones del Prado, 1992. 

D'aquesta manera podem estudiar l'estructura de qualsevol mena d'obra,  no tan sols figurativa,  sinó també abstracte, informal, i tant bidimensionals com tridimensionals.

Anàlisi d'una obra abstracta de E. Warner,  1978.

La figura poligonal del PENTÀGON REGULAR conté una sèrie de relacions entre segments que coincideixen amb la proporció àuria.